セキュリティと暗号
前年(訳注: 2019年)のセキュリティとプライパシーの講義はコンピューターの ユーザー としてどのようによりセキュアにできるかという点に注目していました。今年は、セキュリティと暗号理論のうち、この講義で先に取り上げたツール群を理解するために関係する事柄に注目します。例えば、Gitにおけるハッシュ関数や、SSHにおける鍵導出関数と対称・非対称鍵の利用についてです。
この講義はより厳密で完全なコンピューターシステムのセキュリティ(6.858)、暗号理論(6.857 and 6.875)コースに代わるものではありません。セキュリティの正式な教育を受けずにセキュリティの仕事をしてはなりません。専門家でなければ、暗号を自作してはいけません。同じことはシステムのセキュリティにも当てはまります。
この講義ではとても簡単に(ただ実用的であると考える)基礎的な暗号理論の扱い方を示します。 どのようにセキュアなシステムや暗号プロトコルを 設計する かを教えるには、この講義は十分ではないでしょうが、 既に利用しているプログラムやプロトコルについて一般的な理解をするのには十分であることを願っています。
エントロピー
Entropy(訳注: 日本語版は「情報量」)は乱雑さの尺度です。例えば、パスワードの強度を判断するときに有用です。
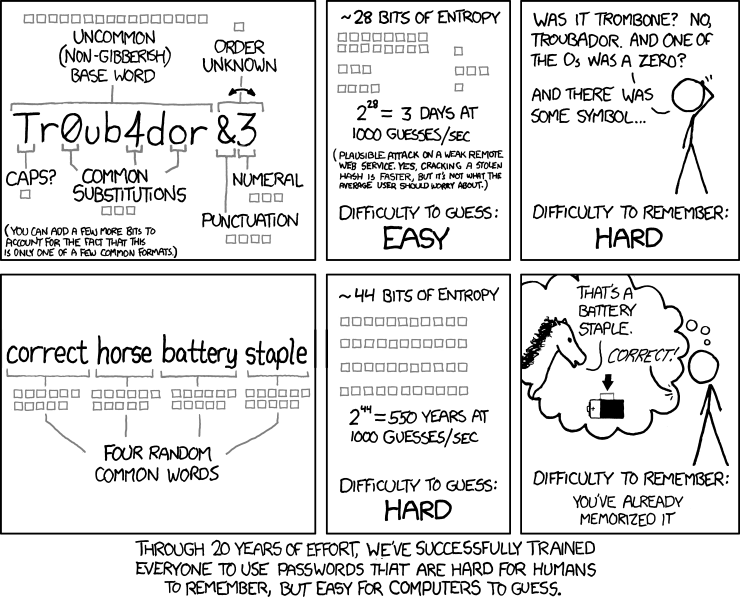
一般的ではない基本の単語 順序はわからないTr0ub4dor&3大文字? よくある置き換え 記号 数字 (これは一般的なフォーマットの一例を示しているだけなので、もう少しビットを増やすことは可能) |
約28ビットのエントロピー 2^28 = 1000試行/sで3日 (脆弱なリモートのWebサービスでは妥当。盗まれたハッシュ値のクラックはもっと速くできるが、一般的なユーザが心配することではない) 当てやすさ: 簡単 |
tromboneだったかな?いやtroubadorだ。Oの一つは0にしたんだったかな?いくつかは記号にしたような… 覚えやすさ: 難しい |
correcthorsebatterystaple 4つのランダムな一般的な単語 |
約44ビットのエントロピー 2^44 = 1000試行/sで550年 当てやすさ: 難しい |
覚えやすさ: もう覚えている |
20年間かけて、人に覚えにくくコンピューターが当てやすいパスワードを使うように人々を訓練してしまった
XKCD comicに描かれているように、”correcthorsebatterystaple”は”Tr0ub4dor&3”よりも強固です。 ではどのように定量的に評価すればよいのでしょうか。
エントロピーは ビット 単位で表現されます。取り得る結果の集合から一様かつランダムに取り出す場合、そのエントロピーはlog_2(結果の選択肢の数)に等しいです。
公平な硬貨投げは1ビットのエントロピーを与えます。6面のサイコロを振ることは約2.58ビットのエントロピーです。
攻撃者はパスワードの 型 は知っているものの、特定のパスワードを選ぶために使用したランダムさ(例えばサイコロを振る)については知らないことを考えるべきでしょう。
エントロピーは何ビットあれば十分でしょうか。それは脅威の種類によります。オンラインで当てるのであれば、XKCDの漫画にあったように40ビットのエントロピーでもまあ良いでしょう。オフラインでの攻撃に耐えるには、80ビットやそれ以上のより強固なパスワードが必要です。
ハッシュ関数
cryptographic hash function(訳注: 日本語版は「暗号学的ハッシュ関数」)は任意のサイズのデータを、固定長で特別な性質を持つデータへとマッピングします。 大まかなハッシュ関数の定義は次のようになります。
hash(value: array<byte>) -> vector<byte, N> (Nはいくつかの定数)
ハッシュ関数の例の一つとして、Gitで使われているSHA1(訳注: 日本語版 SHA-1)があります。任意のサイズの入力を160ビットの出力(16進数では40桁で表される)へと変換します。sha1sumコマンドを使ってSHA-1ハッシュを試してみることができます。
$ printf 'hello' | sha1sum
aaf4c61ddcc5e8a2dabede0f3b482cd9aea9434d
$ printf 'hello' | sha1sum
aaf4c61ddcc5e8a2dabede0f3b482cd9aea9434d
$ printf 'Hello' | sha1sum
f7ff9e8b7bb2e09b70935a5d785e0cc5d9d0abf0
概念としてはハッシュ関数は逆算することが難しく、ランダムであるように見える(が決定論的)な関数と考えることができます。これはハッシュ関数の概念的なモデル(Random oracle/日本語版ランダムオラクル)にあたります。ハッシュ関数は次の性質を持ちます。
- 決定論的: 同一の入力は常に同一の出力を生成する
- 非可逆: ある出力
hに対してhash(m) = hを満たす入力mを見つけることが困難 - 弱衝突耐性: 入力
m_1が与えられたとき、hash(m_1) = hash(m_2)を満たす別の入力m_2を見つけることが困難 - 強衝突耐性:
hash(m_1) = hash(m_2)となる2つの入力m_1をm_2を見つけることが困難(これは弱衝突耐性よりも強い性質であることに注意)
注: 一定の役割では機能するものの、SHA-1はもはや強固な暗号論的ハッシュ関数ではないと考えられています。暗号論的ハッシュ関数の寿命の表は興味深いでしょう。しかし、特定のハッシュ関数を勧めることはこの講義の範囲を越えています。このような作業をする必要がある場合、正式なセキュリティや暗号理論のトレーニングを受ける必要があります。
応用
- Gitはファイルの内容を示すために使用しています。ここでのハッシュ関数(訳注: 日本語版「ハッシュ関数」)はより一般的な概念です。どうしてGitは暗号論的ハッシュ関数を使用したのでしょうか?
- ファイルの内容の要約として。LinuxのISOファイルのようなソフトウェアは(信頼性が低い可能性のある)ミラーからダウンロードされることがあります。ハッシュを使ってミラーが信頼できる必要性をなくせます。公式サイトにはダウンロードリンク(第三者のミラーを指している)と並んでハッシュが載っていることが多いので、ファイルのダウンロードが終わってからそのハッシュと比較すればよいのです。
- コミットメント方式(訳注: 日本語版「ビットコミットメント」)。ある値をコミットしたいが、その値そのものを明かすのは後にしたい場合を考えます。例えば、二者が同時に見られるコインなしに、公正なコイントスを「頭の中で」したいとします。私が値
r = random()を選んで、h = sha256(r)のハッシュ値を共有します。あなたは裏か表か宣言します(偶数のrは表、奇数のrは裏を示すことに合意します)。宣言したあと、私はrを公開することができ、sha256(r)の値が先に共有したハッシュ値を一致することを確認することでずるをしていないことを確認できます。
鍵導出関数
暗号論的ハッシュに関連して、Key derivation function(KDF, 日本語版「鍵導出関数」は他の暗号アルゴリズムで使用する固定長の出力を得ることを含め、多くの応用があります。一般に、鍵導出関数はオフラインの総当たり攻撃を遅くするために意図的に遅くされています。
応用
- 他の暗号アルゴリズムで使用する鍵をパスフレーズから生成する。例えば下記に示す対称暗号があります。
- ログイン情報の保存。平文でパスワードを保存するのは好ましくありません。正しい方法はランダムなSalt(訳注: 日本語版「ソルト」)
salt = random()をユーザごとに生成、保存して、KDF(password + salt)を保存することです。ログイン試行の検証は入力されたパスワードと保存されたソルトの値から、再度KDFを算出することにより行います。
対称暗号
暗号理論について考えたとき、メッセージの内容を隠すことは最初に思い浮かぶことでしょう。 対称暗号は次の関数の組でこれを実現します。
keygen() -> key (この関数はランダム化されている)
encrypt(plaintext: array<byte>, key) -> array<byte> (暗号文)
decrypt(ciphertext: array<byte>, key) -> array<byte> (平文)
暗号化関数は得られる出力(暗号文)から入力(平文)を鍵なしには決められないような性質を持っています。復号関数は明らかな性質であるdecrypt(encrypt(m, k), k) = mを持ちます。
現在幅広く用いられている対称暗号の例としてAES(訳注: 日本語版「Advanced Encryption Standard」)があります。
応用
- 信用できないクラウドサービスに保存するファイルを暗号化します。KDFと組み合わせて、ファイルをパスフレーズで暗号化することによります。鍵を
key = KDF(passphrase)で生成し、encrypt(file, key)により得られる暗号化ファイルを保存します。
非対称暗号
「非対称」は異なる役割の2つの鍵が存在することを示します。 秘密鍵はその名前からわかるように秘密にしておくものです。一方で、公開鍵は公開して共有することができて、それによってセキュリティ上の影響を受けることがありません。これは対称暗号において鍵を共有する方法とは異なります。 非対称暗号は次のように暗号化、復号と署名、検証の関数を提供します。
keygen() -> (public key, private key) (この関数はランダム化されている)
encrypt(plaintext: array<byte>, public key) -> array<byte> (暗号文)
decrypt(ciphertext: array<byte>, private key) -> array<byte> (平文)
sign(message: array<byte>, private key) -> array<byte> (署名)
verify(message: array<byte>, signature: array<byte>, public key) -> bool (署名が正当であるか否か)
暗号化、復号の機能は対称暗号のそれと似た性質を持っています。
メッセージは 公開 鍵を用いて暗号化することができます。得られた出力(暗号文)から 秘密 鍵なしには入力(平文)を決定することは困難です。復号関数は明らかな性質decrypt(encrypt(m, public key), private key) = mを持ちます。
対称暗号と非対称暗号は物理的な鍵に例えることができます。 対称暗号はドアの鍵のようなものです。鍵を持つ人は誰でも鍵をかけ、また外すことができます。 非対称暗号は南京錠のようなものです。誰かに開いた状態の南京錠(公開鍵)を渡し、メッセージを箱に入れて鍵をかけた後は、鍵(秘密鍵)を持つあなただけが鍵を開けられるようになります。
署名、検証の関数は物理的な署名に期待するのと同様に、偽造が困難という性質を持っています。
メッセージの内容によらず、 秘密 鍵なしにはverify(message, signature, public key)が真となるような署名を生成することは困難です。
もちろん、検証関数は明らかな性質であるverify(message, sign(message, private key), public key) = trueとなる性質を持っています。
応用
- PGPによるメールの暗号化(訳注: 日本語版Pretty Good Privacy)。公開鍵をオンラインで公開(PGPキーサーバやKeybase)している人に対して、誰でも暗号化されたメールを送れます。
- 秘匿化されたメッセージング。SignalやKeybaseのようなアプリは秘匿化された通信路を確立するために非対称暗号を使っています。
- ソフトウェアへの署名。GitはGPGで署名されたコミットやタグを持つことができます。公開鍵と併せて投稿されれば、誰でもダウンロードしたソフトウェアの正当性を検証することができます。
鍵の配布
非対称鍵は素晴らしいものですが、公開鍵を配布し、実世界のアイデンティティと関連付ける大きな課題もあります。 この課題の解決策はいくつもあります。Signalは単純な解決策を提供します。最初に利用するときに検証し、アプリの外で公開鍵の交換を行えるようになっています(友達の「安全番号」を対面で確認します)。 PGPは信用の輪(訳注: 日本語版「信用の輪(Web of Trust)」)と呼ばれる別の解決策を提供します。 Keybaseはsocial proofとその他の適切な考えに基づく解決策を提供します。
それぞれのモデルにメリットがありますが、我々(講師陣)はKeybaseのモデルが好みです。
ケーススタディ
パスワードマネージャ
これは誰もが試すべき必須のツールです。例として、KeePassXC, pass, 1Passwordが挙げられます。 パスワードマネージャを使うと、全てのログイン情報を個別かつランダムに生成されエントロピーの高いパスワードにして、また全てのパスワードを一カ所にまとめておくことができます。パスワード群は対称暗号で暗号化されます。暗号化に使うキーは、パスフレーズからKDFを用いて生成されます。
パスワードマネージャを使えば、パスワードの使い回しを避け、あるサイトから漏洩したときの影響を小さくすることができます。また、エントロピーの高いパスワードを使えるので推測されてしまう可能性を下げます。覚えておく必要があるのはエントロピーの高いパスワード(訳注: パスワードマネージャのファイルの暗号化に使うマスターパスワード)一つのみです。
2要素認証
2要素認証 (訳注: 2Factor-Authenticationの頭文字から2FAとも呼ばれる。日本語版「多要素認証」)はパスフレーズ(「知る要素」)と同時に、2要素認証認証機(例えばYubiKey、「持つ要素」)を要求します。 これにより、パスワードの流出やフィッシング(訳注: 日本語版「フィッシング」)から守ります。
ディスク全体の暗号化
ノートパソコンのディスク全体が暗号化された状態にしておくことは、盗まれてしまったときにデータを守る簡単な方法です。Linuxではcryptsetup + LUKS、WindowsではBitLocker、macOSではFileVaultが使えます。パスフレーズによって保護されたキーを使って、ディスク全体を対称暗号で暗号化します。
メッセージの秘匿
SignalまたはKeybaseを使います。エンドツーエンドのセキュリティは非対称暗号によるプロセスから始まります。ここで、連絡先の公開鍵を取得することは重要なステップです。高いセキュリティを実現するために、公開鍵を通信以外の手段で認証する(SignalやKeybaseの場合)か、social proofを信用する(Keybase)ことが求められます。
SSH
先の講義でSSHとSSH鍵の利用について触れました。暗号の観点から見てみましょう。
ssh-keygenを実行すると、公開鍵と秘密鍵の非対称な鍵ペアが生成されます。OSが提供するエントロピー(ハードウェアイベントの収集等を基にする)を使って、ランダムに生成されます。公開鍵は秘密にしておく必要性が低いので、そのまま保存されます。一方で、秘密鍵は暗号化してディスクに保存すべきです。ssh-keygenはユーザにパスフレーズを入力するよう要求しますが、これは鍵導出関数に送られ、生成されたキーによって秘密鍵は対称暗号で暗号化されます。
SSHを使用するときは、サーバが一度クライアントの公開鍵を知ればそれは.ssh/authorized_keysファイルに保存されます。接続しようとするクライアントは非対称署名を利用してその正当性を証明することができます。これはチャレンジレスポンスによってなされます。
チャレンジレスポンスの概要を示します。サーバは乱数を選び、クライアントに送ります。クライアントはそれに署名し、サーバへ送り返します。サーバは署名と記録されている公開鍵が対応することを確認します。これは事実上、クライアントがサーバの.ssh/authorized_keys にある公開鍵に対応する秘密鍵を持っていることを証明するので、サーバはクライアントのログインを許可することができます。
資料
- 前年(2019年)の講義ノート: コンピュータのユーザとしてのセキュリティやプライバシーを中心とした内容でした
- Cryptographic Right Answers: 「Xにはどの暗号を使うべきか?」という疑問の答えが多数載っています
演習
- エントロピー
- 辞書に載っている小文字の単語を4つ選び、パスワードとしたときを考えます。
辞書の単語数は100,000で、単語の選択に偏りはないものとします。
パスワードの例は
correcthorsebatterystapleです。 このようなパスワードのエントロピーは何bitあるでしょうか。 - パスワードを決める別の方法として、8桁のランダムな英数字(大文字と小文字の両方)を使います。
例えば
rg8Ql34gです。 これのエントロピーは何bitでしょうか。 - より強いパスワードはどちらでしょうか。
- 攻撃者は1秒間に10,000件のパスワードを試行できるとします。それぞれのパスワードを破るために必要な平均所要時間を求めてください。
- 辞書に載っている小文字の単語を4つ選び、パスワードとしたときを考えます。
辞書の単語数は100,000で、単語の選択に偏りはないものとします。
パスワードの例は
- 暗号論的ハッシュ関数 Debianのイメージをミラーサイト(例えば アルゼンチンのミラーサイト)からダウンロードします。
sha256sumコマンドを使用して得られたハッシュ値と、Debianの公式サイトから得られるハッシュ値(debian.orgにあるSHA256のハッシュファイル)が一致することを確認します。 - 対称暗号 OpenSSLを使って、ファイルをAESで暗号化します:
openssl aes-256-cbc -salt -in {input filename} -out {output filename}。暗号化したファイルの内容をcatやhexdumpで確認します。復号するコマンドはopenssl aes-256-cbc -d -in {input filename} -out {output filename}です。元々の内容と一致することをcmpを使って確認します。 - 非対称暗号
- アクセスする必要のあるコンピュータでSSH鍵ペアの設定を行います(KerberosがSSH鍵に干渉するため、MITのAthena以外で)。リンク先のチュートリアルではRSAを使用していますが、よりセキュアなED25519を使いましょう(訳注:
ssh-keygen -t ed25519のようにする)。秘密鍵は安全に保存されるよう、パスフレーズで暗号化されていることを確認します。 - GPGのセットアップ
- Anishへ暗号化されたメールを送る(公開鍵)
- Gitのコミットを
git commit -Sを使って署名したり、署名付のタグをgit tag -sにより作ります。 コミットの署名はgit show --show-signature、タグはgit tag -vにより確認できます。
- アクセスする必要のあるコンピュータでSSH鍵ペアの設定を行います(KerberosがSSH鍵に干渉するため、MITのAthena以外で)。リンク先のチュートリアルではRSAを使用していますが、よりセキュアなED25519を使いましょう(訳注:
Licensed under CC BY-NC-SA.